Old school vs new school and the fundamental theorem of poker

Daniel Negreanu, a top professional poker player since the 1990s, has a youtube series where he breaks down poker hands according to how they were played ‘old school’ style, versus how they would be played today, ‘new school’. By ‘new school’ he is referring to a relatively recent period, the last 10 years or so, in particular since the advent of computer solvers.
Contrast this with the game of chess, where grandmasters regularly play openings invented hundreds of years ago. Of course they are much stronger players than their predecessors — chess computers have helped them find new ideas too — but many concepts have stood the test of time. A lot of poker theory from 10 or 20 years ago, however, is now known to be outright wrong.
The fundamental theorem of poker
David Sklansky, in his book ‘the theory of poker’ (new edition 1999) stated that Every time you play a hand differently from the way you would have played it if you could see all your opponents’ cards, they gain; and every time you play your hand the same way you would have played it if you could see all their cards, they lose.
This wasn’t a throw away line in his book. This was his fundamental theorem, oft repeated. And on one level it’s difficult to argue with. If we are facing a river bet that happens to be a bluff, then we would call if you could see the opponent’s cards. Conversely, if we played differently from the way we would have played if we could see their cards, we would make the mistake of folding to that bluff. The fundamental theorem is a bit of mouthful, I know, but seems to make perfect sense.
The problem with this view is that its natural corollary is that poker is in essence a game of deception. Is it though?
A poker toy game
As a quick digression, let’s consider a very simple version of poker, a ‘toy game’. I can bet $0, $1 or $2, and you have to call. We then deal out 5 cards, Texas holdem style, and we see who wins. Then, to make it fair, it’s your turn to bet $0, $1 or $2 and I have to call. What is the optimal strategy? This game is simple enough that the solution is fairly obvious: bet $0 when the equity (probability of winning) of your hole cards is less than 50%, bet $2 when your equity is more than 50%, and never bet $1.
Ok, it’s not a very exciting game; you won’t find it played in card rooms around the country. But it does suggest that when we have pocket Aces in the normal full version of Texas holdem, that we want to raise (and hopefully have the opportunity to 3-bet and 4-bet) preflop. When we have the best hand in poker we want to play for as much money as possible, and we want to get the money in while we’re ahead.
I believe the reason I see players in my recreational poker group limping in with pocket Aces pre-flop is that they are trying to be deceptive. Ok, maybe I’m mostly preaching to the converted with respect to Aces. But it still seems to be a popular strategy to shovel money into the pot when we are weak but slow-playing when we have a strong hand (i.e. the opposite of how a bright 6 year old, who’s just learned the rules, might approach the game). Players are showing belief in the fundamental theorem of poker.
The computer solver theory of poker
The ‘new school’ game theory optimal (GTO) theory of poker takes a different tack. All players are completely transparent about the hands they might hold. All pre-flop ranges are known and all bet sizes on future streets are specified. The computer then solves for check, bet, call, raise (etc) frequencies at every decision point (‘node’) in the game tree. The resulting strategy is made fully transparent to the opponent too! Yet the opponent cannot exploit it, as the solver’s overall strategy is completely balanced and unexploitable.
Here’s a random example of a solver output for a player in position who has been checked to on a flop of AK3, where the pot is 15 units.
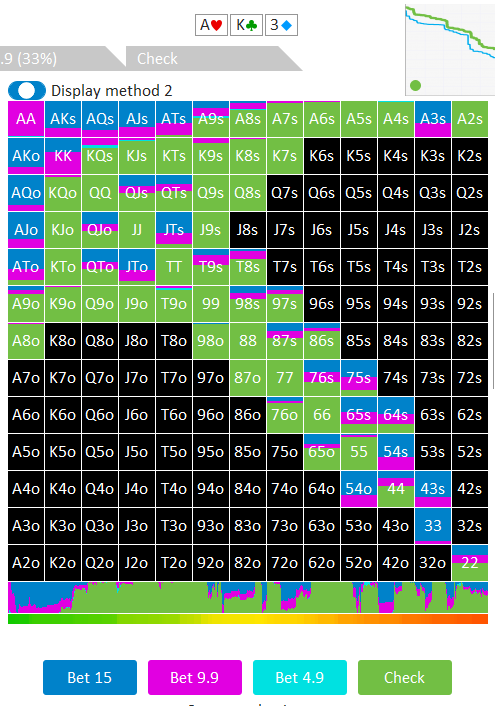
Pocket Aces and pocket Kings are a pure bet (though, interestingly, AA bets 2/3 of pot and not 100% pot). Hero does not try to deceive the opponent into thinking that he doesn’t have pocket Aces, but rather balances it by betting 76s, say (a weak hand) at some frequency for the same amount.
But isn’t betting the weak hand ‘deception’?
New school poker doesn’t think in terms of deception, but rather in terms of equity vs expected value (EV). Equity is the raw probability of winning, assuming no more money goes into the pot and the hand goes to showdown. EV is the value of the hand considering the strategies of all players in the hand, allowing for folds and new money.
Strong hands have high equity and high EV (indeed the EV can be higher than the current size of the pot). Bad hands have low equity and low EV - but the EV can often exceed the equity because we can use these hands to bluff. Medium strength hands often underperform their equity in poker (EV < equity), particularly when out of position.
The GTO approach tends to build the betting range around the strong hands. First decide how the strong hands want to bet, and then choose the best bluffs or semi-bluffs to balance these against. Play the medium strength hands passively.
But I still want to play my pocket Aces deceptively . .
Trust me, it’s a terrible idea. The most generous interpretation is that we have competing incentives when we have pocket Aces (or any other strong hand for that matter): to bet for maximum value versus to deceive the opponents into thinking we are weak and bluff into us. Unless we can confidently rely on our opponents to do our betting for us, the incentive to bet is surely stronger.
It’s worth noting that while betting shows strength, calling also shows strength. If we get a flop that’s good enough to play for stacks, and we’re lucky enough to get a maniac opponent betting into us, by the time we have called down to the river it will be clear that we like our hand.
One possible strategy is to limp with pocket Aces in early position, in the hope that someone will raise us and we can 3-bet them. This would never happen in GTO land (there is no limping in early position), but it’s a reasonable strategy against a recreational player pool. It’s only deceptive for one round of bidding though. Once we make that 3-bet the gig is up!
Opening wide pre-flop
To belabour the point on this one, limping in 80% of the time pre-flop is a poor strategy, whether we’re old school or new school! Sure, playing is more fun than folding, but if poker were like chess and opening weak hands led to rapid and certain loss, players would stop doing it, pronto.
Poker is a game of repeated scenarios (‘spots’). There isn’t much time to make a decision, so players will rely on heuristics — rules of thumb. These ‘strategies’ might be intricate in the hands of a pro, and simple (not to mention surprisingly terrible) in the case of a recreational player.
One would think that the game of poker taps into our basic human understanding of risk and reward, such that we would settle on fairly good heuristics. Against that is that there is so much variance in the game that players can adopt poor strategies without ever learning the error of their ways.
GTO strategy wouldn’t generally recommend limping at all — it’s raise or fold — as it’s difficult to raise some hands and limp others without resulting in a very weak limping range. One strategy is to limp those pocket Aces. It’s true that this strengthens and protects our limping range, but at the huge cost of losing value from those pocket Aces. Better to tighten up that limping range by folding out the weaker hands.
Other old school thinking
Old school thinking included a number of heuristics that haven’t stood the test of time.
An example is betting simply to ‘retain the betting lead’. This is not really a thing. You only have the betting lead if you have the range advantage. Another heuristic is betting to ‘take down the pot’. Betting for protection is solver approved, but betting 3* the pot because we want to win it there & then is not ‘a thing’. Finally, leading out or ‘donk betting’ used to be seen as a fish (beginner) move, but there are certain circumstances where the board so favours the preflop caller that donk betting is solver approved.
So is new school thinking the final answer?
I’m personally not so sure that the new school paradigm is always that helpful. In chess most good moves will be good against any opposition, and likewise bad moves will be inadvisable against opposition that’s strong or weak. In poker we can play a poor strategy, but our opponents’ even worse strategy may make the play good!
For example, betting 3 times the pot with 2 pair when we see a flush draw in order to ‘take down the pot’ is bad strategy. Everyone (except the guy with a set) will fold and we’ll leave money on the table. But if our opponents are so bad that they call anyway, then it becomes a good strategy again!
If our opponents are VPIPing (putting money in the pot preflop) 80% of the time, it seems absurd to open under the gun only 15% of the time, the solver approved frequency. Opening 60% of the time will almost guarantee victory in the long run, even if the rest of the strategy is no superior to theirs. In the unlikely event that our opponents react by opening 40% of the time henceforth, then we can react and open 30% of the time. If these reactions continue, enough iterations will eventually bring us to GTO.
Commentators try to square the circle by saying we should follow GTO as a baseline, but then try to exploit our opponents when they (inevitably) deviate from the GTO strategy. It’s not obvious to me that the first step is even necessary: uncover the population tendencies and adopt the strategy that works best against that . .
I’m pretty confident that this strategy will involve playing pocket Aces aggressively, though, against almost any player pool!