Poker: a Flush beats a Straight

When our monthly poker game first started out, my buddy RF would lean over conspiratorially and ask, “so does a flush beat a straight, or is it the other way around”? When I say ‘started out’ I mean the first couple of years. He was 90% sure, I’m sure, but confirmation never hurts. Following a few tens of thousands of online hands during the pandemic years, RF no longer has to ask this question. He still needs work on many other aspects of his game however.
Just to set expectations, this blog is more a Probability 101 musing than a poker theory discussion, so if you like combinations and permutations, read on . .
It’s generally explained that a flush beats a straight in Texas holdem because the probability of flopping a flush (0.20%) is lower than the probability of flopping a straight (0.39%). The lower probability outcome earns the higher ranking.
It doesn’t have to be this way. The game would still ‘work’ if poker officialdom decreed that a straight beat a flush. Players would simply adjust to the changed incentives by valuing their connected starting cards relatively higher than suited cards. There are many card games where the rewards of an outcome aren’t in relation to the probability of their occurance. Think of games that have a Joker, or major suits vs minor suits in bridge.
Is it surprising that a flush still beats a straight if 7 cards instead of 5 cards are dealt? Given we see 7 cards at showdown in Texas holdem, not 5, this is really the probability we should be examining:

We see that the probabilities after 7 cards still follow the given rankings, though the flush probability is now closer to 2/3 than 1/2 of the straight probability. It is worth noting that it’s quite difficult to end up with a high card only (17.4%). Following our stated ranking criterion, not even being able to make a pair at showdown should really rank higher than 2 pair . .
Now let’s imagine a poker variant that has further streets, so that 8 cards, 9 cards, 10 cards, etc, are dealt. Is it the case that flushes are always more rare than straights? No! I ran a simulation in python to investigate this, and it turns out that once 12+ cards are dealt, straights should be ranked higher than flushes:
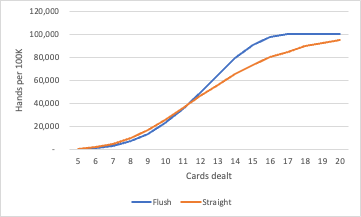
Note that the above counts all straights and flushes, even if they are also straight flushes or royal flushes, as these make up circa 10% of hands once 18 cards are dealt.
A common sense explanation for the above finding is that when the number of cards dealt is close to 5, the computation is dominated by the number of ways (combinations) that we can deal a flush vs a straight with 5 cards (5.1k ways vs 10.2k ways). However, as the number of cards dealt increases the computation is dominated by the number of ways of avoiding a flush or straight. To avoid a flush with 16 cards, you need to be dealt 4 of each suit. With the 17th card you have to make a flush. On the other hand you can be dealt up to 40 cards without ever making a straight (if you never get dealt a 5, Ten or Ace, say).
Just for a laugh, here is the frequency of all hand types, as the number of cards dealt increases (here I’ve excluded straight and royal flushes from the straight and flush tally):

By the time we’re dealt 40 cards we are just left with royal flushes, straight flushes and four of a kind (leaving aside how this game would work with just 1 pack, unless we are playing solitaire .. ).
We are accustomed to a standard pack of cards having 4 suits and 13 ranks, 52 cards in total. If we played a variant of poker that had 3 suits and 17 ranks (51 total), then this would reduce the probability of a 5 card straight in 5 cards from 0.39% to 0.14%. The probability of a flush would increase from 0.20% to 0.79%. Poker officialdom would need to rank a straight higher than a flush.
If changing the deck dimensions seems fanciful, there is a variant of poker called “short-deck holdem”, which has been played at the highest level (Phil Ivey won $617k at the Triton Super High Roller tournament in 2018 playing short deck holdem). This game is played with the 2s through 5s of a standard deck removed, leaving just 4 suits of 9 ranks (36 cards total). This increases the probability of a full house to higher than the probability of a flush, hence in this game a flush ranks higher than a full house. Otherwise the rules of the game are the same as standard Texas holdem.
Wikipedia also notes, ‘In theory, three-of-a-kind ranks higher than a straight as the probability of achieving three-of-a-kind is lower than a straight in short-deck, however recent games have been ranking straight higher than three-of-a-kind which has become standard.’ As I noted at the beginning of this article, poker officialdom doesn’t need to follow the probabilities in setting the hand rankings for the game to ‘work’.
So would it be so ridiculous for poker officialdom to say that a straight beats a flush? Note that if a player gets dealt cards of the same suit, then the probability of flopping a flush jumps from 0.20% to 0.84%, which is higher than any hole cards that aren’t connected (eg 76). Hole cards that have 1 ‘gap’, only have a 0.82% of flopping a straight.
Furthermore, if we start with suited cards, hearts say, and the flop includes 2 hearts, then we have 9 possibilities to get that 5th heart to make a flush. If we flop an open ended straight draw, on the other hand, we only have 8 possibilities to make a straight. Generally speaking, there are more ways to ‘back into’ a straight: there are many combinations of gut shot straights that we’ll probably end up having to fold.
This illustrates the difference between raw equity and expected value (EV) in poker: straights may have the higher probability of occuring than flushes if taken to showdown (i.e. raw equity). But given the multiple rounds of betting of Texas holdem, flushes may actually win more money (EV), suggesting they should be downgraded in the hand rankings. I’m not saying this is conclusive: straights have the benefit of being more disguised than flushes allowing straights to win the occasional big pot. When there are 3 of the same suit on the board everyone becomes wary that a flush is possible. I’ll leave the question open.
If I can offer one piece of poker strategy from this article, suited cards are much better than unsuited hole cards! Although KJs only has 2–3% more raw equity than KJo, it has much more playability and hence superior EV. This is assuming of course that your poker school hasn’t decided that, for tonight only, a straight does after all beat a flush!